The questions in this section are intended to test your knowledge and skills on biostatistics, literature evaluation and interpretation of medical journals. All board of pharmacy specialties (bps) exam will have some biostatistics.
Click on the right arrow to go to the next question. If the arrow is missing hover your mouse to the lower right, above the ad until the mouse is clickable.
BPS Biostatistics Practice Questions
Congratulations - you have completed BPS Biostatistics Practice Questions.
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
In a study where rivaroxaban was compared to enoxaparin to find total venous thromboembolism(VTE) following hip replacement surgery, there were 17 total VTE out of 1513 patients in the rivaraoaban group and 57 total VTE out of 1473 patient in the enoxaparin group. What is the relative risk reduction of using rivaroxaban over enoxaparin?
39% | |
71% | |
29% | |
14% | |
42% |
Question 1 Explanation:
Relative risk reduction: 0.71 = 71%
Relative risk: (Event rate in rivaroxaban group)/(Event rate in enoxaparin group) = (17/1513)/(57/1473) = 0.2903
Relative risk reduction: 1 – (relative risk) = 1 – 0.2903 = 0.7097 = 0.71
Reference:
I. Barratt A, Wyer PC, Hatala R, et al. Tips for learners of evidence-based medicine: 1. Relative risk reduction, absolute risk reduction and number needed to treat. CMAJ. 2004;171(4):353-8. doi: 10.1503/cmaj.1021197.
II. Stone N, Robinson J, Lichtenstein A et al. 2013 ACC/AHA Guideline on the Treatment of Blood Cholesterol to Reduce Atherosclerotic Cardiovascular Risk in Adults. Circulation. 2013;129(25 suppl 2):S1-S45. doi:10.1161/01.cir.0000437738.63853.7a.
Relative risk: (Event rate in rivaroxaban group)/(Event rate in enoxaparin group) = (17/1513)/(57/1473) = 0.2903
Relative risk reduction: 1 – (relative risk) = 1 – 0.2903 = 0.7097 = 0.71
Reference:
I. Barratt A, Wyer PC, Hatala R, et al. Tips for learners of evidence-based medicine: 1. Relative risk reduction, absolute risk reduction and number needed to treat. CMAJ. 2004;171(4):353-8. doi: 10.1503/cmaj.1021197.
II. Stone N, Robinson J, Lichtenstein A et al. 2013 ACC/AHA Guideline on the Treatment of Blood Cholesterol to Reduce Atherosclerotic Cardiovascular Risk in Adults. Circulation. 2013;129(25 suppl 2):S1-S45. doi:10.1161/01.cir.0000437738.63853.7a.
Question 2 |
Which of the following is/are ordinal data?
NYHA I-IV | |
Sex | |
Improvement Yes/No | |
Grade of breast cancer | |
Alive or Dead |
Question 2 Explanation:
Categorical data includes ordinal (ordered categories) and nominal (unordered categories). NYHA I-IV and grade of breast cancer are considered ordinal data because the categories for the answer choice are in order, you can have NYHA class I, II, III, or IV. Grade of breast cancers are also in order, grade 1, 2, or 3. Sex, Improvemnet Yes/No, Alive or Dead is considered nominal, unordered data because the answer choices are female or male, and do not have a set order.
Reference:
"Statistics at Square One | The BMJ". Bmj.com. 2016. Web. 7 Nov. 2016. Available at: http://www.bmj.com/about-bmj/resources-readers/publications/statistics-square-one
Reference:
"Statistics at Square One | The BMJ". Bmj.com. 2016. Web. 7 Nov. 2016. Available at: http://www.bmj.com/about-bmj/resources-readers/publications/statistics-square-one
Question 3 |
In normal distribution, what percentage of the sample is found within 2 standard deviation of the mean?
68% | |
95% | |
99% | |
100% | |
72% |
Question 3 Explanation:
In a normal distribution sample, within 1 standard deviation 68% of the sample falls within 1 standard deviation, 95% within 2 standard deviations, and 99.7% within 3 standard deviations of the mean.
Reference:
I. "Mean, Mode And Median - Measures Of Central Tendency - When To Use With Different Types Of Variable And Skewed Distributions | Laerd Statistics". statistics.laerd.com. 2016. Web. 7 Nov. 2016. Available at: https://statistics.laerd.com/statistical-guides/measures-central-tendency-mean-mode-median.php
II. "Statistics at Square One | The BMJ". Bmj.com. 2016. Web. 7 Nov. 2016. Available at: http://www.bmj.com/about-bmj/resources-readers/publications/statistics-square-one
Reference:
I. "Mean, Mode And Median - Measures Of Central Tendency - When To Use With Different Types Of Variable And Skewed Distributions | Laerd Statistics". statistics.laerd.com. 2016. Web. 7 Nov. 2016. Available at: https://statistics.laerd.com/statistical-guides/measures-central-tendency-mean-mode-median.php
II. "Statistics at Square One | The BMJ". Bmj.com. 2016. Web. 7 Nov. 2016. Available at: http://www.bmj.com/about-bmj/resources-readers/publications/statistics-square-one
Question 4 |
Which of the following is dichotomous variable?
Sex | |
Pain yes/ Pain no | |
NYHA I-IV | |
alive / dead | |
Grade of Breast Cancer |
Question 4 Explanation:
Dichotomous data is considered categorical data that only has two categories, or two answer choices. All 3 answer choices have only 2 categories: sex has male or female, pain is yes or no, and alive or dead is only two options also.
Reference:
"Statistics at Square One | The BMJ". Bmj.com. 2016. Web. 7 Nov. 2016. Available at: http://www.bmj.com/about-bmj/resources-readers/publications/statistics-square-one
Reference:
"Statistics at Square One | The BMJ". Bmj.com. 2016. Web. 7 Nov. 2016. Available at: http://www.bmj.com/about-bmj/resources-readers/publications/statistics-square-one
Question 5 |
In the US Nurses’ Health Study (NHS) cohort study, where they looked at association of regular aspirin use (≥two 325 mg tablets/week) and colorectal cancer in 82,911 women found (RR, 0.77; 95% CI, 0.67–0.88) over 20 years of follow-up. What does this say about the mortality from colorectal cancer?
Those who takes aspirin ≥2 times/week have 23% lower risk of colorectal cancer | |
Those who takes aspirin ≥2 times/week have 0.77% lower risk of colorectal cancer | |
Those who takes aspirin ≥2 times/week have 77% lower risk of colorectal cancer | |
Those who takes aspirin ≥2 times/week have 0.23% reduction in death from colorectal cancer
| |
None of the above is correct |
Question 5 Explanation:
Relative risk can be stated as 0.77 times as likely or 0.77 times the risk, but it could also be illustrated as a relative risk reduction and stated as a 23% risk reduction or 23% lower risk by taking the medication.
Reference:
Irwig, Les. Chapter 18: Relative risk, relative and absolute risk reduction, number needed to treat and confidence intervals. Smart health choices: making sense of health advice. Judy Irwig, 2007. Retrieved Jan. 24, 2017 from: https://www.ncbi.nlm.nih.gov/books/NBK63647/
Reference:
Irwig, Les. Chapter 18: Relative risk, relative and absolute risk reduction, number needed to treat and confidence intervals. Smart health choices: making sense of health advice. Judy Irwig, 2007. Retrieved Jan. 24, 2017 from: https://www.ncbi.nlm.nih.gov/books/NBK63647/
Question 6 |
The rate that an outcome will occur given a particular exposure, compared to the rate of the outcome occurring in the absence of that exposure is definition of which of the following?
Incidence rate | |
Prevalence rate | |
Odds ratio | |
Relative risk
| |
Confidence Interval |
Question 6 Explanation:
RR = rate of an outcome occurring in an exposed group (treatment group/intervention group) divided by the rate of an outcome occurring in an unexposed group (control group)
Ex: Relative Risk = Rate of UTI in patients taking drug XYZ / rate of UTI in patients not on drug XYZ
Reference:
I. 2x2 Contingency Table with Odds Ratios, etc. (n.d.). Retrieved Jan. 24, 2017 from: http://www.vassarstats.net/odds2x2.html
II. Szumilas, M. "Explaining odds ratios." J Can Acad Child Adolesc Psychiatry 19 (2010): 227. Retrieved Jan. 24, 2017 from: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2938757/
Reference:
I. 2x2 Contingency Table with Odds Ratios, etc. (n.d.). Retrieved Jan. 24, 2017 from: http://www.vassarstats.net/odds2x2.html
II. Szumilas, M. "Explaining odds ratios." J Can Acad Child Adolesc Psychiatry 19 (2010): 227. Retrieved Jan. 24, 2017 from: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2938757/
Question 7 |
Results from a Meta-analysis where they looked at frequency of postoperative arterial fibrillation in patients on Ascorbic acid after cardiac surgery found odds ratio, 0.44 (95% CI, 0.32 to 0.61). How can you interpret this data?
Ascorbic acid increased frequency of postoperative arterial fibrillation after cardiac surgery by 44% | |
Ascorbic acid decreased frequency of postoperative arterial fibrillation after cardiac surgery by 44% | |
There was no statistically significant difference in frequency of postoperative arterial fibrillation after cardiac surgery | |
Ascorbic acid decreased frequency of postoperative arterial fibrillation after cardiac surgery by 56% | |
None of the above are correct |
Question 7 Explanation:
Odds ratio of 0.44 (44%) means that this group was associated with an event happening 44% of the time, compared to 1 (an event happening 100% of the time if unexposed), therefore 100 - 44 = 56%, which is the reduction caused by the exposure. Exposure is the use of ascorbic acid.
Reference:
Davies, Huw Talfryn Oakley, Iain Kinloch Crombie, and Manouche Tavakoli. "When can odds ratios mislead?." Bmj 316.7136 (1998): 989-991. Retrieved Jan. 24, 2017 from: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1112884/
Reference:
Davies, Huw Talfryn Oakley, Iain Kinloch Crombie, and Manouche Tavakoli. "When can odds ratios mislead?." Bmj 316.7136 (1998): 989-991. Retrieved Jan. 24, 2017 from: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1112884/
Question 8 |
Number of new cases per population at risk in a given time period is a definition of which of the following?
Incidence rate
| |
Prevalence rate | |
Mortality rate
| |
Odds ratio
| |
Confidence Interval |
Question 8 Explanation:
Incidence rate = New reported cases / summed person-years of observation (avg population during time interval). Prevalence = Cases in a population in a given time period / total population at that time Mortality rate = deaths during specified time interval / population size at risk for death
Reference:
Dicker, R. C., Coronado, F., Koo, D., et al. Principals of Epidemiology in Public Health Practice, Third Edition: An Introduction to Applied Epidemiology and Biostatistics; Lesson 3, Section 2. Oct. 2006 Retrieved Jan. 24, 2017 from: https://www.cdc.gov/ophss/csels/dsepd/ss1978/lesson3/section2.html Updated: Nov. 2011
Reference:
Dicker, R. C., Coronado, F., Koo, D., et al. Principals of Epidemiology in Public Health Practice, Third Edition: An Introduction to Applied Epidemiology and Biostatistics; Lesson 3, Section 2. Oct. 2006 Retrieved Jan. 24, 2017 from: https://www.cdc.gov/ophss/csels/dsepd/ss1978/lesson3/section2.html Updated: Nov. 2011
Question 9 |
In the US Nurses’ Health Study (NHS) cohort study, where they looked at association of regular aspirin use (≥two 325 mg tablets/week) and colorectal cancer in 82,911 women found (RR, 0.77; 95% CI, 0.67–0.88) over 20 years of follow-up. In an another analysis of the NHS, regular aspirin use, investigator also found (hazard ratio [HR]=0.72, 95% CI 0.56–0.92), what does this say about the mortality from colorectal cancer? How can this data best be interpreted?
Those who takes aspirin regularly have 72% lower risk of colorectal cancer | |
Those who takes aspirin regularly have 28% reduction in death from colorectal cancer
| |
Those who takes aspirin regularly have 0.23% lower risk of colorectal cancer
| |
Those who takes aspirin regularly have 77% lower risk of colorectal cancer |
Question 9 Explanation:
Hazard ratio can be used to compare time-to-event data between 2 groups. In this case the time to event was 20 years-to-death from colorectal cancer and the groups were patients taking aspirin 325mg 2 or more times a week and patients that did not. With the HR being 0.72, the patients taking the aspirin were 0.72 times likely to die at any time during the 20 years. This means that aspirin had a 28% reduction in death from colorectal cancer, 1 – 0.72 = 0.28.
Reference:
Sedgwick, Philip, and Katherine Joekes. "Interpreting hazard ratios." BMJ: British Medical Journal 351 (2015).
Reference:
Sedgwick, Philip, and Katherine Joekes. "Interpreting hazard ratios." BMJ: British Medical Journal 351 (2015).
Question 10 |
In a publication, observed mean weight of 200 patients was reported as 69.4 ±9.3 kg. If 9.3 kg is the SEM (standared error of mean), calculate the SD (standared deviation) and variance?
131.52kg/17298kg | |
78.7kg/9.3kg | |
87.24kg/69.4kg | |
69.4kg/131kg |
Question 10 Explanation:
SEM x √n = SD
9.3 x √200 = 131.52 kg = SD
SD2 (square) = variance
131.522 = 17298 kg = variance
Reference:
Statistics at Square One The BMJ". Bmj.com. 2016. Web. 7 Nov. 2016. Available at: http://www.bmj.com/about-bmj/resources-readers/publications/statistics-square-one
9.3 x √200 = 131.52 kg = SD
SD2 (square) = variance
131.522 = 17298 kg = variance
Reference:
Statistics at Square One The BMJ". Bmj.com. 2016. Web. 7 Nov. 2016. Available at: http://www.bmj.com/about-bmj/resources-readers/publications/statistics-square-one
Question 11 |
Which of the following is/are nominal data?
Sex | |
Blood group | |
Race | |
A, B and C. |
Question 11 Explanation:
Nominal data is considered unordered categories. Sex answers fall into male or female which is unordered. Race can be multiple answers such as Caucasian, African American, Asian, etc which is unordered. Blood group can only have blood type O, A, B, or AB which is also unordered. Ordered, or ordinal data would have categories that are in some sort of order.
Reference:
I. "Statistics at Square One | The BMJ". Bmj.com. 2016. Web. 7 Nov. 2016. Available at: http://www.bmj.com/about-bmj/resources-readers/publications/statistics-square-one
Reference:
I. "Statistics at Square One | The BMJ". Bmj.com. 2016. Web. 7 Nov. 2016. Available at: http://www.bmj.com/about-bmj/resources-readers/publications/statistics-square-one
Question 12 |
The mean decrease in Heart Rate after initiating a beta blocker XYZ in 90 patients was 24 beat per minute with standard error of 3.78 beats for minute. What would be the 95% confidence interval for the decrease in HR after initiating drug XYZ?
16.64-31.4mmHg | |
20.22-27.78mmHg | |
14.55-33.45mmHg | |
22.28-26.28 mmHg |
Question 12 Explanation:
24 + (1.96 x 3.78) = 31.4 mmHg
24 - (1.96 x 3.78) = 16.6 mmHg
The 95% confidence interval is from 16.6 mmHg to 31.4 mmHg, which means we can be 95% sure that the mean decrease in HR after starting beta blocker XYZ of the population falls within this range. You can also say that there is a 5% chance that the mean decrease in HR of the population falls outside of this range.
Reference:
I. "Statistics at Square One | The BMJ". Bmj.com. 2016. Web. 7 Nov. 2016. Available at: http://www.bmj.com/about-bmj/resources-readers/publications/statistics-square-one
24 - (1.96 x 3.78) = 16.6 mmHg
The 95% confidence interval is from 16.6 mmHg to 31.4 mmHg, which means we can be 95% sure that the mean decrease in HR after starting beta blocker XYZ of the population falls within this range. You can also say that there is a 5% chance that the mean decrease in HR of the population falls outside of this range.
Reference:
I. "Statistics at Square One | The BMJ". Bmj.com. 2016. Web. 7 Nov. 2016. Available at: http://www.bmj.com/about-bmj/resources-readers/publications/statistics-square-one
Question 13 |
In a cohort study where the investigators looked at the association between smoking and throat cancer for 20 years found the relative risk of 14. How can this data best be interpreted?
14% of the throat cancers are due to smoking
| |
Smokers had 14% increased risk of throat cancer compared to non-smokers
| |
Smokers had 14 times the risk of throat cancer compared to non-smokers
| |
Smokers had 86% increased risk of throat cancer compared to non-smoker
|
Question 13 Explanation:
Relative risk is a proportion so when interpreting relative risk one can say “times as,” in this case it is 14 times the risk or is 14 times as likely.
Reference:
Irwig, Les. Chapter 18: Relative risk, relative and absolute risk reduction, number needed to treat and confidence intervals. Smart health choices: making sense of health advice. Judy Irwig, 2007. Retrieved Jan. 24, 2017 from: https://www.ncbi.nlm.nih.gov/books/NBK63647/
Reference:
Irwig, Les. Chapter 18: Relative risk, relative and absolute risk reduction, number needed to treat and confidence intervals. Smart health choices: making sense of health advice. Judy Irwig, 2007. Retrieved Jan. 24, 2017 from: https://www.ncbi.nlm.nih.gov/books/NBK63647/
Question 14 |
Study that looked at mortality after Dronedarone Therapy for Severe Heart Failure.
Given the data above what is the absolute risk of cardiovascular death with Dronedarone group in severe heart failure patients?0.033 | |
0.077 | |
0.13 | |
0.77 |
Question 14 Explanation:
Absolute risk: 0.077
(Cardiovascular death with Dronedarone)/(Total in Dronedarone group) = 24/310 = 0.077419
Reference:
Barratt A, Wyer PC, Hatala R, et al. Tips for learners of evidence-based medicine: 1. Relative risk reduction, absolute risk reduction and number needed to treat. CMAJ. 2004;171(4):353-8. doi: 10.1503/cmaj.1021197.
(Cardiovascular death with Dronedarone)/(Total in Dronedarone group) = 24/310 = 0.077419
Reference:
Barratt A, Wyer PC, Hatala R, et al. Tips for learners of evidence-based medicine: 1. Relative risk reduction, absolute risk reduction and number needed to treat. CMAJ. 2004;171(4):353-8. doi: 10.1503/cmaj.1021197.
Question 15 |
Study that looked at mortality after Dronedarone Therapy for Severe Heart Failure.
What is the relative risk of cardiovascular death using Dronedarone therapy compared to placebo?2.7 | |
1.7 | |
97.3 | |
98.3 |
Question 15 Explanation:
Relative risk: 2.7
(Event rate in Dronedarone group)/(Event rate in Placebo group) = (24/310)/(9/317) = 2.72688
Reference:
Barratt A, Wyer PC, Hatala R, et al. Tips for learners of evidence-based medicine: 1. Relative risk reduction, absolute risk reduction and number needed to treat. CMAJ. 2004;171(4):353-8. doi: 10.1503/cmaj.1021197.
(Event rate in Dronedarone group)/(Event rate in Placebo group) = (24/310)/(9/317) = 2.72688
Reference:
Barratt A, Wyer PC, Hatala R, et al. Tips for learners of evidence-based medicine: 1. Relative risk reduction, absolute risk reduction and number needed to treat. CMAJ. 2004;171(4):353-8. doi: 10.1503/cmaj.1021197.
Question 16 |
Study that looked at mortality after Dronedarone Therapy for Severe Heart Failure
What is the absolute risk of cardiovascular death in placebo group in severe heart failure patients?0.077 | |
0.082 | |
0.028 | |
0.033 |
Question 16 Explanation:
Absolute risk: 0.028
(Cardiovascular death with Placebo)/(Total in Placebo group) = 9/317 = 0.02839
Reference:
Barratt A, Wyer PC, Hatala R, et al. Tips for learners of evidence-based medicine: 1. Relative risk reduction, absolute risk reduction and number needed to treat. CMAJ. 2004;171(4):353-8. doi: 10.1503/cmaj.1021197.
(Cardiovascular death with Placebo)/(Total in Placebo group) = 9/317 = 0.02839
Reference:
Barratt A, Wyer PC, Hatala R, et al. Tips for learners of evidence-based medicine: 1. Relative risk reduction, absolute risk reduction and number needed to treat. CMAJ. 2004;171(4):353-8. doi: 10.1503/cmaj.1021197.
Question 17 |
Study that looked at mortality after Dronedarone Therapy for Severe Heart Failure
What is the relative risk increase using Dronedarone compared to placebo in severe heart failure patients?170% | |
30% | |
6.9% | |
4.9% |
Question 17 Explanation:
Relative risk increase: 1.7 = 170%
1 – (relative risk) =
1 – 2.72688 = - 1.72688
Reference:
Barratt A, Wyer PC, Hatala R, et al. Tips for learners of evidence-based medicine: 1. Relative risk reduction, absolute risk reduction and number needed to treat. CMAJ. 2004;171(4):353-8. doi: 10.1503/cmaj.1021197.
1 – (relative risk) =
1 – 2.72688 = - 1.72688
Reference:
Barratt A, Wyer PC, Hatala R, et al. Tips for learners of evidence-based medicine: 1. Relative risk reduction, absolute risk reduction and number needed to treat. CMAJ. 2004;171(4):353-8. doi: 10.1503/cmaj.1021197.
Question 18 |
Results from a case-control study where they assessed whether a drug is associated with decrease in weight showed odds ratio for weight change 0.7 (95% CI, 0.6-1.2). How can this data best be interpreted?
The drug increase weight by 30% | |
The drug decrease weight by 30% | |
The drug decrease weight by 70% | |
The data inconclusive to whether the drug is associated with change in weight
|
Question 18 Explanation:
When the 95% CI spans 1 (the null) the results may not be significant. These results would suggest a look into the p-value to determine the significance of these results.
Reference:
Szumilas, M. "Explaining odds ratios." J Can Acad Child Adolesc Psychiatry 19 (2010): 227. Retrieved Jan. 24, 2017 from:https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2938757
Reference:
Szumilas, M. "Explaining odds ratios." J Can Acad Child Adolesc Psychiatry 19 (2010): 227. Retrieved Jan. 24, 2017 from:https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2938757
Question 19 |
In the ARISTOTLE Study the rate of death from any cause was 3.52% in Apixaban group per year Vs 3.94% in warfarin group. HR 0.89; 95% CI, 0.80 to 0.99. Which of the following statement is true based on the given information?
The rate of death from any cause was lower in the Apixaban group than in Warfarin group. | |
The rate of death from any cause was not significant in the Apixaban group Vs Warfarin group. | |
Warfarin had significantly lower rate of death compared to Apixaban. | |
Since there is no p value no conclusion can be drawn from the given data |
Question 19 Explanation:
A Is correct because the rate of death is significant as indicated by the 95% CI does not contain the value 1. So it is appropriate to make a statement: The rate of death from any cause was lower in the Apixaban group than in Warfarin group the meaning of 1 in a confidence ration indicates that the risk reduction in the outcome is the same between the two groups. Answer C is wrong because the rate of death in the warfarin group was higher than the rate in the Apixaban group (3.94% vs 3.52% perspectively). Answer D is wrong because although there is no p value listed, statistical significance can still be inferred from a 95% confidence interval, which is presented here as 0.80 to 0.99.
Reference:
Windish DM, Huot SJ, Green ML. Medicine resident’s understanding of the biostatistics and results in the medical literature. JAMA 2007;298:1010-22.
Reference:
Windish DM, Huot SJ, Green ML. Medicine resident’s understanding of the biostatistics and results in the medical literature. JAMA 2007;298:1010-22.
Question 20 |
In the ARISTOTLE Study the rate of the primary outcome was 1.27% per year in the Apixaban group, as compared with 1.60% per year in the Warfarin group (hazard ratio with Apixaban, 0.79; 95% confidence interval [CI], 0.66 to 0.95; P<0.001 for noninferiority. The primary objective was to determine whether Apixaban was noninferior to Warfarin in reducing the rate of stroke (ischemic or hemorrhagic) or systemic embolism among patients with atrial fibrillation and at least one other risk factor for stroke. Which of the following statement is true based on the given information?
Apixaban is superior to warfarin in reducing rate of stroke or systemic embolism among patients with atrial fibrillation. | |
Apixaban is as effective as warfarin in reducing rate of stroke or systemic embolism among patients with atrial fibrillation. | |
Apixaban is more effective than warfarin in reducing rate of stroke but not systemic embolism among patients with atrial fibrillation | |
Apixaban is superior to warfarin in reducing rate of stroke but warfarin is noninferior in reducing systemic embolism among patients with atrial fibrillation. |
Question 20 Explanation:
Answer A is incorrect because presented p-value is for noninferiority, not for superiority. Based on the given information, no conclusions about superiority can be made. Answer B. is correct. The p-value provided is for noninferiority, it can be concluded that Apixaban is as effective as warfarin in reducing rate of stroke or systemic embolism among patients with atrial fibrillation. Answer C is incorrect. Stroke and systemic embolism were combined into one primary outcome here for this confidence interval, so more information is needed to determine which agent did better for the specific type of event, either stroke or systemic embolism. Answer D. is incorrect because the rate of the primary outcome was higher in the warfarin group compared to the Apixaban group, meaning stroke or systemic embolism occurred more so in the warfarin group. For the same reason as with C, these two events are represented as combined into one primary outcome and more information would be needed.
Reference: I. Windish DM, Huot SJ, Green ML. Medicine resident’s understanding of the biostatistics and results in the medical literature. JAMA 2007;298:1010-22.
Reference: I. Windish DM, Huot SJ, Green ML. Medicine resident’s understanding of the biostatistics and results in the medical literature. JAMA 2007;298:1010-22.
Question 21 |
In a study where Rivaroxaban was compared to Enoxaparin to find total VTE following HIP replacement surgery, there were 17 total VTE out of 1513 patients in the Rivaraoaban group and 57 total VTE out of 1473 patient in the enoxaparin group. What is the absolute risk reduction of using Rivaroxaban over Enoxaparin?
17 | |
57 | |
71 | |
2.7 |
Question 21 Explanation:
Absolute risk reduction: 0.027 = 2.7%
(Event rate in enoxaparin group) – (Event rate in rivaroxaban group) = (57/1473) – (17/1513) = 0.02746
Reference:
Barratt A, Wyer PC, Hatala R, et al. Tips for learners of evidence-based medicine: 1. Relative risk reduction, absolute risk reduction and number needed to treat. CMAJ. 2004;171(4):353-8. doi: 10.1503/cmaj.1021197.
(Event rate in enoxaparin group) – (Event rate in rivaroxaban group) = (57/1473) – (17/1513) = 0.02746
Reference:
Barratt A, Wyer PC, Hatala R, et al. Tips for learners of evidence-based medicine: 1. Relative risk reduction, absolute risk reduction and number needed to treat. CMAJ. 2004;171(4):353-8. doi: 10.1503/cmaj.1021197.
Question 22 |
Which of the following is/are Categorical data?
Age | |
Sex | |
Better/Same /Worse | |
B and C. |
Question 22 Explanation:
Categorical data includes ordinal (ordered categories) and nominal (unordered categories). Age is not categorical because age can fall under any continuous number, so it is considered quantitative, continuous data. Sex is nominal categorical data. Better/same/worse is considered ordinal categorical since the answers fall in order.
Reference:
"Statistics at Square One | The BMJ". Bmj.com. 2016. Web. 7 Nov. 2016. Available at: http://www.bmj.com/about-bmj/resources-readers/publications/statistics-square-one
Reference:
"Statistics at Square One | The BMJ". Bmj.com. 2016. Web. 7 Nov. 2016. Available at: http://www.bmj.com/about-bmj/resources-readers/publications/statistics-square-one
Question 23 |
There were total of 510 cases of syphilis with 106 reported new case of syphilis in Dresner County in 2015. The population of Dresner County in 2015 was 410,200 people.
What is the incidence proportion of syphilis in 2015 in Dresner County?
0.026% | |
0.153% | |
0.051% | |
0.015% |
Question 23 Explanation:
Incidence proportion = New reported cases / initial population at risk
Incidence proportion = 106 / (410,200 – 510) = 0.000259 x 100 = 0.026%
Reference:
Dicker, R. C., Coronado, F., Koo, D., et al. Principals of Epidemiology in Public Health Practice, Third Edition: An Introduction to Applied Epidemiology and Biostatistics; Lesson 3, Section 2. Oct. 2006 Retrieved Jan. 24, 2017 from: https://www.cdc.gov/ophss/csels/dsepd/ss1978/lesson3/section2.html Updated: Nov. 2011
Incidence proportion = 106 / (410,200 – 510) = 0.000259 x 100 = 0.026%
Reference:
Dicker, R. C., Coronado, F., Koo, D., et al. Principals of Epidemiology in Public Health Practice, Third Edition: An Introduction to Applied Epidemiology and Biostatistics; Lesson 3, Section 2. Oct. 2006 Retrieved Jan. 24, 2017 from: https://www.cdc.gov/ophss/csels/dsepd/ss1978/lesson3/section2.html Updated: Nov. 2011
Question 24 |
There were total of 510 cases of syphilis with 106 reported new case of syphilis in Dresner County in 2015. The population of Dresner County is 410,200 people.
What is the incidence rate of syphilis in 2015 in Dresner County?
2.6 cases per 10,000 person-years | |
2.3 cases per 10,000 person-years | |
2 cases per 10,000 person-years | |
3.2 cases per 10,000 person-years |
Question 24 Explanation:
Incidence rate = New reported cases / summed person-years of observation (avg population during time interval)
410,200 – 510 = 409,690 – 106 = 409,584
Incidence rate = 106 / (409,584 + ½ 106) = 2.6 cases per 10,000 person-years
Reference:
Dicker, R. C., Coronado, F., Koo, D., et al. Principals of Epidemiology in Public Health Practice, Third Edition: An Introduction to Applied Epidemiology and Biostatistics; Lesson 3, Section 2. Oct. 2006 Retrieved Jan. 24, 2017 from: https://www.cdc.gov/ophss/csels/dsepd/ss1978/lesson3/section2.html Updated: Nov. 2011
410,200 – 510 = 409,690 – 106 = 409,584
Incidence rate = 106 / (409,584 + ½ 106) = 2.6 cases per 10,000 person-years
Reference:
Dicker, R. C., Coronado, F., Koo, D., et al. Principals of Epidemiology in Public Health Practice, Third Edition: An Introduction to Applied Epidemiology and Biostatistics; Lesson 3, Section 2. Oct. 2006 Retrieved Jan. 24, 2017 from: https://www.cdc.gov/ophss/csels/dsepd/ss1978/lesson3/section2.html Updated: Nov. 2011
Question 25 |
Proportion of people in a population who have a particular disease at a specified point in time or over a specified period of time is definition as which of the following?
Incidence rate | |
Prevalence rate | |
Mortality rate | |
Relative risk |
Question 25 Explanation:
Incidence rate = New reported cases / summed person-years of observation (avg population during time interval)
Prevalence = Cases in a population in a given time period / total population at that time
Reference:
I. Dicker, R. C., Coronado, F., Koo, D., et al. Principals of Epidemiology in Public Health Practice, Third Edition: An Introduction to Applied Epidemiology and Biostatistics; Lesson 3, Section 2. Oct. 2006 Retrieved Jan. 24, 2017 from: https://www.cdc.gov/ophss/csels/dsepd/ss1978/lesson3/section2.html Updated: Nov. 2011
II. Numerators, denominators and populations at risk. Jun. 20, 2010. Retrieved Jan. 24, 2017 from: http://www.healthknowledge.org.uk/public-health-textbook/research-methods/1a-epidemiology/numerators-denominators-populations
Reference:
I. Dicker, R. C., Coronado, F., Koo, D., et al. Principals of Epidemiology in Public Health Practice, Third Edition: An Introduction to Applied Epidemiology and Biostatistics; Lesson 3, Section 2. Oct. 2006 Retrieved Jan. 24, 2017 from: https://www.cdc.gov/ophss/csels/dsepd/ss1978/lesson3/section2.html Updated: Nov. 2011
II. Numerators, denominators and populations at risk. Jun. 20, 2010. Retrieved Jan. 24, 2017 from: http://www.healthknowledge.org.uk/public-health-textbook/research-methods/1a-epidemiology/numerators-denominators-populations
Question 26 |
In a cohort study of 47,363 male US health professionals, the Health Professionals Follow-up Study (HPFS), regular aspirin use (≥2 times/week) found (RR, 0.79; 95% CI, 0.69–0.90) for colorectal cancer over 18 years of follow-up. How can this data best be interpreted?
I) Those who takes aspirin ≥2 times/week have 0.79 times the risk of colorectal cancer
II) Those who takes aspirin ≥2 times/week have 0.21 times the risk of colorectal cancer
III) Those who takes aspirin ≥2 times/week have 21% lower risk of colorectal cancer
IV) Those who takes aspirin ≥2 times/week have 79% lower risk of colorectal cancer
II
| |
II and III | |
I and IV | |
I and III
|
Question 26 Explanation:
Relative risk can be stated as 0.79 times as likely or 0.79 times the risk, but it could also be illustrated as a relative risk reduction and stated as a 21% risk reduction or 21% lower risk by taking the medication.
Reference:
I. Irwig, Les. Chapter 18: Relative risk, relative and absolute risk reduction, number needed to treat and confidence intervals. Smart health choices: making sense of health advice. Judy Irwig, 2007. Retrieved Jan. 24, 2017 from: https://www.ncbi.nlm.nih.gov/books/NBK63647/ II. Confidence Intervals for the Risk Ratio (Relative Risk). (n.d.) Retrieved Jan. 24, 2017 from: http://sphweb.bumc.bu.edu/otlt/mph-modules/bs/bs704_confidence_intervals/bs704_confidence_intervals8.html
Reference:
I. Irwig, Les. Chapter 18: Relative risk, relative and absolute risk reduction, number needed to treat and confidence intervals. Smart health choices: making sense of health advice. Judy Irwig, 2007. Retrieved Jan. 24, 2017 from: https://www.ncbi.nlm.nih.gov/books/NBK63647/ II. Confidence Intervals for the Risk Ratio (Relative Risk). (n.d.) Retrieved Jan. 24, 2017 from: http://sphweb.bumc.bu.edu/otlt/mph-modules/bs/bs704_confidence_intervals/bs704_confidence_intervals8.html
Question 27 |
The rate that an outcome will occur given a particular exposure, compared to the rate of the outcome occurring in the absence of that exposure is definition of which of the following?
Incidence rate | |
Prevelance rate
| |
Odds ratio | |
Relative risk |
Question 27 Explanation:
RR = rate of an outcome occurring in an exposed group (treatment group/intervention group) divided by the rate of an outcome occurring in an unexposed group (control group)
Ex: Relative Risk = Rate of UTI in patients taking drug XYZ / rate of UTI in patients not on drug XYZ
Reference:
2x2 Contingency Table with Odds Ratios, etc. (n.d.). Retrieved Jan. 24, 2017 from: http://www.vassarstats.net/odds2x2.html
Ex: Relative Risk = Rate of UTI in patients taking drug XYZ / rate of UTI in patients not on drug XYZ
Reference:
2x2 Contingency Table with Odds Ratios, etc. (n.d.). Retrieved Jan. 24, 2017 from: http://www.vassarstats.net/odds2x2.html
Question 28 |
Number of new cases per population at risk in a given time period is a definition of which of the following?
Incidence rate
| |
Prevalence rate | |
Mortality rate
| |
Odds ratio |
Question 28 Explanation:
Incidence rate = New reported cases / summed person-years of observation (avg population during time interval). Prevalence = Cases in a population in a given time period / total population at that time Mortality rate = deaths during specified time interval / population size at risk for death
Reference:
Dicker, R. C., Coronado, F., Koo, D., et al. Principals of Epidemiology in Public Health Practice, Third Edition: An Introduction to Applied Epidemiology and Biostatistics; Lesson 3, Section 2. Oct. 2006 Retrieved Jan. 24, 2017 from: https://www.cdc.gov/ophss/csels/dsepd/ss1978/lesson3/section2.html Updated: Nov. 2011
Reference:
Dicker, R. C., Coronado, F., Koo, D., et al. Principals of Epidemiology in Public Health Practice, Third Edition: An Introduction to Applied Epidemiology and Biostatistics; Lesson 3, Section 2. Oct. 2006 Retrieved Jan. 24, 2017 from: https://www.cdc.gov/ophss/csels/dsepd/ss1978/lesson3/section2.html Updated: Nov. 2011
Question 29 |
In a study where the investigators measured decrease in weight in 120 patients after 90 days of initiating this hypothetical drug, the mean decrease in weight was 16 pounds with standard error of mean 4.2 pounds, what is the 95% confidence interval for the decrease in weight with this drug? What is the Interpretation of this Confidence interval?
8.23-24.23pounds | |
11.8-27.8pounds
| |
9.5-26.5pounds | |
12.4-18.4 pouds |
Question 29 Explanation:
16 + (1.96 x 4.2) = 24.23pounds.
16 - (1.96 x 4.2) = 8.23pounds.
The 95% confidence interval is from 8.23 pounds to 24.23pounds, which means we can be 95% sure that the mean decrease in weight after initiating the drug falls within this range. You can also say that there is a 5% chance that the mean decrease in weight of the population falls outside of this range.
Reference:
"Statistics At Square One | The BMJ". Bmj.com. 2016. Web. 7 Nov. 2016. Available at: http://www.bmj.com/about-bmj/resources-readers/publications/statistics-square-one
16 - (1.96 x 4.2) = 8.23pounds.
The 95% confidence interval is from 8.23 pounds to 24.23pounds, which means we can be 95% sure that the mean decrease in weight after initiating the drug falls within this range. You can also say that there is a 5% chance that the mean decrease in weight of the population falls outside of this range.
Reference:
"Statistics At Square One | The BMJ". Bmj.com. 2016. Web. 7 Nov. 2016. Available at: http://www.bmj.com/about-bmj/resources-readers/publications/statistics-square-one
Question 30 |
In a publication observed mean weight of 200 patients was reported as 69.4 ±9.3 kg. If 9.3 kg is the SD, calculate the SEM?
60.1kg
| |
0.658kg | |
9.3kg | |
17.94kg |
Question 30 Explanation:
SEM = SD/square root of n.
SEM = 9.3 /square root of 200.
= 0.658 kg
Reference:
"Statistics at Square One | The BMJ". Bmj.com. 2016. Web. 7 Nov. 2016. Available at: http://www.bmj.com/about-bmj/resources-readers/publications/statistics-square-one
SEM = 9.3 /square root of 200.
= 0.658 kg
Reference:
"Statistics at Square One | The BMJ". Bmj.com. 2016. Web. 7 Nov. 2016. Available at: http://www.bmj.com/about-bmj/resources-readers/publications/statistics-square-one
Question 31 |
In a study where they measured decrease in weight in 120 patients after 90 days of initiating this hypothetical drug, the mean decrease in weight was 16 pounds with standard error of mean 4.2 pounds, what is the 95% confidence interval for the decrease in weight with this drug? What is the Interpretation of this Confidence interval?
8.23-24.23pounds | |
11.8-27.8pounds | |
9.5-26.5pounds | |
12.4-18.4 pounds |
Question 31 Explanation:
16 + (1.96 x 4.2) = 24.23pounds
16 - (1.96 x 4.2) = 8.23pounds
The 95% confidence interval is from 8.23 pounds to 24.23pounds, which means we can be 95% sure that the mean decrease in weight after initiating the drug falls within this range. You can also say that there is a 5% chance that the mean decrease in weight of the population falls outside of this range.
Reference:
"Statistics at Square One | The BMJ". Bmj.com. 2016. Web. 7 Nov. 2016. Available at: http://www.bmj.com/about-bmj/resources-readers/publications/statistics-square-one
16 - (1.96 x 4.2) = 8.23pounds
The 95% confidence interval is from 8.23 pounds to 24.23pounds, which means we can be 95% sure that the mean decrease in weight after initiating the drug falls within this range. You can also say that there is a 5% chance that the mean decrease in weight of the population falls outside of this range.
Reference:
"Statistics at Square One | The BMJ". Bmj.com. 2016. Web. 7 Nov. 2016. Available at: http://www.bmj.com/about-bmj/resources-readers/publications/statistics-square-one
Question 32 |
In a study, out of 100 children 50 were given nutritional drink supplement twice a day and 50 were not given nutritional drink supplement. After 30 days of the trial, weight increase was measured.
Which of the following is dependent variable?
Nutritional drink supplement or No nutritional drink supplement | |
Number of days | |
Sex | |
Weight |
Question 32 Explanation:
Dependent variable is the variable measured in response to the independent variable, which is what the researcher manipulates. In this example, the independent variable is whether the child was given nutritional supplement or not. The dependent variable is weight, which is what is measured in response.
Reference:
"Statistics at Square One | The BMJ". Bmj.com. 2016. Web. 7 Nov. 2016. Available at: http://www.bmj.com/about-bmj/resources-readers/publications/statistics-square-one "Independent & Dependent Variables". Www2.uncp.edu. 2016. Web. 7 Nov. 2016. Available at: http://www2.uncp.edu/home/collierw/ivdv.htm
Reference:
"Statistics at Square One | The BMJ". Bmj.com. 2016. Web. 7 Nov. 2016. Available at: http://www.bmj.com/about-bmj/resources-readers/publications/statistics-square-one "Independent & Dependent Variables". Www2.uncp.edu. 2016. Web. 7 Nov. 2016. Available at: http://www2.uncp.edu/home/collierw/ivdv.htm
Question 33 |
In a study, out of 100 children 50 were given nutritional drink supplement twice a day and 50 were not given nutritional drink supplement. After 30 days of the trial, weight increase was measured. Which of the following is independent variable?
Nutritional drink supplement or No nutritional drink supplement | |
Number of days | |
Sex | |
Weight |
Question 33 Explanation:
Dependent variable is the variable measured in response to the independent variable, which is what the researcher manipulates. In this example, the independent variable is whether the child was given nutritional supplement or not. The dependent variable is weight, which is what is measured in response.
Reference:
"Statistics at Square One | The BMJ". Bmj.com. 2016. Web. 7 Nov. 2016. Available at: http://www.bmj.com/about-bmj/resources-readers/publications/statistics-square-one "Independent & Dependent Variables". Www2.uncp.edu. 2016. Web. 7 Nov. 2016. Available at: http://www2.uncp.edu/home/collierw/ivdv.htm
Reference:
"Statistics at Square One | The BMJ". Bmj.com. 2016. Web. 7 Nov. 2016. Available at: http://www.bmj.com/about-bmj/resources-readers/publications/statistics-square-one "Independent & Dependent Variables". Www2.uncp.edu. 2016. Web. 7 Nov. 2016. Available at: http://www2.uncp.edu/home/collierw/ivdv.htm
Question 34 |
In a study where Rivaroxaban was compared to enoxaparin to find total VTE following HIP replacement surgery, there were 17 total VTE out of 1513 patients in the Rivaraoaban group and 57 total VTE out of 1473 patient in the enoxaparin group.
How many patients would you need to treat with rivaroxaban rather than enoxaparin to prevent 1 VTE event?
27 | |
63 | |
36 | |
72 |
Question 34 Explanation:
Answer C. Number needed to treat: 36
1/(absolute risk reduction) =
1/0.02746 = 36.4166 = 36
Reference
Barratt A, Wyer PC, Hatala R, et al. Tips for learners of evidence-based medicine: 1. Relative risk reduction, absolute risk reduction and number needed to treat. CMAJ. 2004;171(4):353-8. doi: 10.1503/cmaj.1021197.
1/(absolute risk reduction) =
1/0.02746 = 36.4166 = 36
Reference
Barratt A, Wyer PC, Hatala R, et al. Tips for learners of evidence-based medicine: 1. Relative risk reduction, absolute risk reduction and number needed to treat. CMAJ. 2004;171(4):353-8. doi: 10.1503/cmaj.1021197.
Question 35 |
Out of the 212 patient with a rare disease, 16 patient died within 3 years period. What is the mortality rate of the disease? Report your answer per 1000 patients.
25 deaths per 1000 population in 3 years. | |
50 deaths per 1000 population in 3 years. | |
75 deaths per 1000 population in 3 years. | |
100 deaths per 1000 population in 3 years. |
Question 35 Explanation:
Mortality rate = deaths during specified time interval / population size at risk for death
Mortality rate = 16 / 212 = 0.075 x 1000 = 75 deaths per 1000 population in 3 years.
Reference:
Dicker, R. C., Coronado, F., Koo, D., et al. Principals of Epidemiology in Public Health Practice, Third Edition: An Introduction to Applied Epidemiology and Biostatistics; Lesson 3, Section 3. Oct. 2006 Retrieved Jan. 24, 2017 from: https://www.cdc.gov/ophss/csels/dsepd/ss1978/lesson3/section3.html Updated: Nov. 2011
Mortality rate = 16 / 212 = 0.075 x 1000 = 75 deaths per 1000 population in 3 years.
Reference:
Dicker, R. C., Coronado, F., Koo, D., et al. Principals of Epidemiology in Public Health Practice, Third Edition: An Introduction to Applied Epidemiology and Biostatistics; Lesson 3, Section 3. Oct. 2006 Retrieved Jan. 24, 2017 from: https://www.cdc.gov/ophss/csels/dsepd/ss1978/lesson3/section3.html Updated: Nov. 2011
Question 36 |
A study looking at osteoporosis in women found 80 out of 100 did not use calcium plus vitamin D developed osteoporosis by age 75 years, compared to 15 out of 100 did use calcium plus vitamin D developed osteoporosis. What is the odds ratio?
4 | |
0.04 | |
0.4 | |
40 |
Question 36 Explanation:
Odds ratio = (exposed cases / unexposed cases) / (exposed non-cases / unexposed non-cases)
Odds ratio = (15/80) / (85/20) = 0.04
Reference:
2x2 Contingency Table with Odds Ratios, etc. (n.d.). Retrieved Jan. 24, 2017 from: http://www.vassarstats.net/odds2x2.html )
Szumilas, M. "Explaining odds ratios." J Can Acad Child Adolesc Psychiatry 19 (2010): 227. Retrieved Jan. 24, 2017 from: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2938757/
Odds ratio = (15/80) / (85/20) = 0.04
Reference:
2x2 Contingency Table with Odds Ratios, etc. (n.d.). Retrieved Jan. 24, 2017 from: http://www.vassarstats.net/odds2x2.html )
Szumilas, M. "Explaining odds ratios." J Can Acad Child Adolesc Psychiatry 19 (2010): 227. Retrieved Jan. 24, 2017 from: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2938757/
Question 37 |
In a study where the investigators looked at drug XYZ to treat diabetes. At the end of the study 257 patients out of 1557 that received drug XYZ were found to have at least 1 UTI whereas 59 patients out of 1625 patients who did not receive drug XYZ were found to have at least 1 UTI. What is the odds ratio and relative risk?
OR=4.5 and RR= 5.2 | |
OR =5.2 and RR= 4.5 | |
OR= 19 and RR= 3.0 | |
OR= 3.0 and RR= 19 |
Question 37 Explanation:
Odds = Number of patients with UTI / Number of patients without UTI
Odds ratio = (257/1300) / (59/1566) = 5.2
Risk Ratio = Rate of UTI in patients taking drug XYZ / rate in patients not on drug XYZ
RR = (257/1557) / (59/1625) = 4.5
Reference:
2x2 Contingency Table with Odds Ratios, etc. (n.d.). Retrieved Jan. 24, 2017 from: http://www.vassarstats.net/odds2x2.html
Szumilas, M. "Explaining odds ratios." J Can Acad Child Adolesc Psychiatry 19 (2010): 227. Retrieved Jan. 24, 2017 from: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2938757/
Odds ratio = (257/1300) / (59/1566) = 5.2
Risk Ratio = Rate of UTI in patients taking drug XYZ / rate in patients not on drug XYZ
RR = (257/1557) / (59/1625) = 4.5
Reference:
2x2 Contingency Table with Odds Ratios, etc. (n.d.). Retrieved Jan. 24, 2017 from: http://www.vassarstats.net/odds2x2.html
Szumilas, M. "Explaining odds ratios." J Can Acad Child Adolesc Psychiatry 19 (2010): 227. Retrieved Jan. 24, 2017 from: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2938757/
Question 38 |
In a study where the investigators looked at drug ABC to treat hypertension. When they looked at the side effect profile they found the odds ratio of hyperkalemia was 1.8 (95% CI, 1.56-1.9). Which of the following statement is true about the study.
Drug ABC is associated with higher risk of hyperkalemia | |
Drug ABC is associated with lower risk of hyperkalemia | |
Drug ABC is not associated with hyperkalemia | |
Drug ABC is associated with higher risk of hypokalemia |
Question 38 Explanation:
Odds ratio = 1: Drug exposure does not affect odds of outcome
Odds ratio > 1: Drug exposure is associated with higher odds of outcome
Odds ratio < 1: Drug exposure is associated with a lower odds of outcome
Reference:
Szumilas, M. "Explaining odds ratios." J Can Acad Child Adolesc Psychiatry 19 (2010): 227. Retrieved Jan. 24, 2017 from: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2938757/
Odds ratio > 1: Drug exposure is associated with higher odds of outcome
Odds ratio < 1: Drug exposure is associated with a lower odds of outcome
Reference:
Szumilas, M. "Explaining odds ratios." J Can Acad Child Adolesc Psychiatry 19 (2010): 227. Retrieved Jan. 24, 2017 from: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2938757/
Question 39 |
Results from a case-control study where they assessed whether a drug is associated with decrease in weight showed odds ratio for weight change 0.7 (95% CI, 0.6-1.2). How can this data best be interpreted?
The drug increase weight by 30% | |
The drug decrease weight by 30% | |
The drug decrease weight by 70% | |
The data inconclusive to whether the drug is associated with change in weight |
Question 39 Explanation:
When the 95% CI spans 1 (the null) the results may not be significant. These results would suggest a look into the p-value to determine the significance of these results.
Reference:
Szumilas, M. "Explaining odds ratios." J Can Acad Child Adolesc Psychiatry 19 (2010): 227. Retrieved Jan. 24, 2017 from: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2938757/
Reference:
Szumilas, M. "Explaining odds ratios." J Can Acad Child Adolesc Psychiatry 19 (2010): 227. Retrieved Jan. 24, 2017 from: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2938757/
Question 40 |
You go in the patient’s rooms to get 6 heart rates (HR) from 6 different patients who are on a particular beta blocker. You get the following heart rates 96, 65, 69, 65, 59, 64 beats per minute.
59, 64, 65, 65, 69, 96
What is the mode HR?
69.7 | |
65 | |
59 | |
96 |
Question 40 Explanation:
Most common value (repeated) =65 bpm
Reference:
"Mean, Mode And Median - Measures Of Central Tendency - When To Use With Different Types Of Variable And Skewed Distributions | Laerd Statistics". Statistics.laerd.com. 2016. Web. 7 Nov. 2016. Available at: https://statistics.laerd.com/statistical-guides/measures-central-tendency-mean-mode-median.php
Reference:
"Mean, Mode And Median - Measures Of Central Tendency - When To Use With Different Types Of Variable And Skewed Distributions | Laerd Statistics". Statistics.laerd.com. 2016. Web. 7 Nov. 2016. Available at: https://statistics.laerd.com/statistical-guides/measures-central-tendency-mean-mode-median.php
Question 41 |
You go in the patient’s rooms to get 6 heart rates (HR) from 6 different patients who are on a particular beta blocker. You get the following heart rates 96, 65, 69, 65, 59, 64 beats per minute.
59, 64, 65, 65, 69, 96
What is the median HR?
69.7 | |
65 | |
59 | |
96 |
Question 41 Explanation:
Middle value =65 bpm
Reference
"Mean, Mode And Median - Measures Of Central Tendency - When To Use With Different Types Of Variable And Skewed Distributions | Laerd Statistics". Statistics.laerd.com. 2016. Web. 7 Nov. 2016. Available at: https://statistics.laerd.com/statistical-guides/measures-central-tendency-mean-mode-median.php
Reference
"Mean, Mode And Median - Measures Of Central Tendency - When To Use With Different Types Of Variable And Skewed Distributions | Laerd Statistics". Statistics.laerd.com. 2016. Web. 7 Nov. 2016. Available at: https://statistics.laerd.com/statistical-guides/measures-central-tendency-mean-mode-median.php
Question 42 |
You go in the patient’s rooms to get 6 heart rates from 6 different patients who are on a particular beta blocker. You get the following heart rates 96, 65, 69, 65, 59, 64 beats per minute.
59, 64, 65, 65, 69, 96
Is the data skewed to the right, left or center?
Right | |
Left | |
Center | |
Middle |
Question 42 Explanation:
Most of the values are around 65 bpm. Because there is one value much higher (96 bpm), this skews the data to the right, or it moves the mean towards the right. Skewed right.
Reference:
"Mean, Mode And Median - Measures Of Central Tendency - When To Use With Different Types Of Variable And Skewed Distributions | Laerd Statistics". Statistics.laerd.com. 2016. Web. 7 Nov. 2016. Available at: https://statistics.laerd.com/statistical-guides/measures-central-tendency-mean-mode-median.php
Reference:
"Mean, Mode And Median - Measures Of Central Tendency - When To Use With Different Types Of Variable And Skewed Distributions | Laerd Statistics". Statistics.laerd.com. 2016. Web. 7 Nov. 2016. Available at: https://statistics.laerd.com/statistical-guides/measures-central-tendency-mean-mode-median.php
Question 43 |
In a study, out of 100 children 50 were given nutritional drink supplement twice a day and 50 were not given nutritional drink supplement. After 30 days of the trial, weight increase was measured.
Which of the following is dependent variable?
Nutritional drink supplement or No nutritional drink supplement | |
Number of days | |
Sex | |
Weight |
Question 43 Explanation:
Answer D. Dependent variable is the variable measured in response to the independent variable, which is what the researcher manipulates. In this example, the independent variable is whether the child was given nutritional supplement or not. The dependent variable is weight, which is what is measured in response.
Reference:
1. "Statistics at Square One | The BMJ". Bmj.com. 2016. Web. 7 Nov. 2016. Available at: http://www.bmj.com/about-bmj/resources-readers/publications/statistics-square-one
Reference:
1. "Statistics at Square One | The BMJ". Bmj.com. 2016. Web. 7 Nov. 2016. Available at: http://www.bmj.com/about-bmj/resources-readers/publications/statistics-square-one
Question 44 |
In a study, out of 100 children 50 were given nutritional drink supplement twice a day and 50 were not given nutritional drink supplement. After 30 days of the trial, weight increase was measured. Which of the following is independent variable?
Nutritional drink supplement or No nutritional drink supplement | |
Number of days | |
Sex | |
Weight |
Question 44 Explanation:
Answer A. Dependent variable is the variable measured in response to the independent variable, which is what the researcher manipulates. In this example, the independent variable is whether the child was given nutritional supplement or not. The dependent variable is weight, which is what is measured in response.
Reference:
1. "Statistics at Square One | The BMJ". Bmj.com. 2016. Web. 7 Nov. 2016. Available at: http://www.bmj.com/about-bmj/resources-readers/publications/statistics-square-one
Reference:
1. "Statistics at Square One | The BMJ". Bmj.com. 2016. Web. 7 Nov. 2016. Available at: http://www.bmj.com/about-bmj/resources-readers/publications/statistics-square-one
Question 45 |
In Gaussian distribution, what percentage of the sample is found within 2.5 standard deviation of the mean?
50% | |
68% | |
95% | |
99% |
Question 45 Explanation:
Answer D. Within 2.5 standard deviations of the mean, 98.8% of the sample falls. Look at the "Bell Curve" Standard Normal Distribution.
Reference:
"Statistics at Square One | The BMJ". Bmj.com. 2016. Web. 7 Nov. 2016. Available at: http://www.bmj.com/about-bmj/resources-readers/publications/statistics-square-one
Reference:
"Statistics at Square One | The BMJ". Bmj.com. 2016. Web. 7 Nov. 2016. Available at: http://www.bmj.com/about-bmj/resources-readers/publications/statistics-square-one
Question 46 |
In Normal distribution, what percentage of the sample is found within 2 standard deviation of the mean?
68% | |
95% | |
99% | |
100% |
Question 46 Explanation:
Answer B. In a normal distribution sample, within 1 standard deviation 68% of the sample falls within 1 standard deviation, 95% within 2 standard deviations, and 99.7% within 3 standard deviations of the mean.
Reference:
1. "Mean, Mode And Median - Measures Of Central Tendency - When To Use With Different Types Of Variable And Skewed Distributions | Laerd Statistics". statistics.laerd.com. 2016. Web. 7 Nov. 2016. Available at: https://statistics.laerd.com/statistical-guides/measures-central-tendency-mean-mode-median.php
Reference:
1. "Mean, Mode And Median - Measures Of Central Tendency - When To Use With Different Types Of Variable And Skewed Distributions | Laerd Statistics". statistics.laerd.com. 2016. Web. 7 Nov. 2016. Available at: https://statistics.laerd.com/statistical-guides/measures-central-tendency-mean-mode-median.php
Question 47 |
You go in the patient’s rooms to get 6 heart rates from 6 different patients on a particular beta blocker. You get the following heart rates 96, 65, 69, 65, 59, 64 beats per minute.
What is the mean HR?
69.7 | |
65 | |
59 | |
96 |
Question 47 Explanation:
Answer A. (59 + 64 + 65 + 65 + 69 + 96) / 6 = 69.7 bpm
Reference:
1. "Mean, Mode And Median - Measures Of Central Tendency - When To Use With Different Types Of Variable And Skewed Distributions | Laerd Statistics". Statistics.laerd.com. 2016. Web. 7 Nov. 2016. Available at: https://statistics.laerd.com/statistical-guides/measures-central-tendency-mean-mode-median.php
2. "Statistics At Square One | The BMJ". Bmj.com. 2016. Web. 7 Nov. 2016. Available at: http://www.bmj.com/about-bmj/resources-readers/publications/statistics-square-one
Reference:
1. "Mean, Mode And Median - Measures Of Central Tendency - When To Use With Different Types Of Variable And Skewed Distributions | Laerd Statistics". Statistics.laerd.com. 2016. Web. 7 Nov. 2016. Available at: https://statistics.laerd.com/statistical-guides/measures-central-tendency-mean-mode-median.php
2. "Statistics At Square One | The BMJ". Bmj.com. 2016. Web. 7 Nov. 2016. Available at: http://www.bmj.com/about-bmj/resources-readers/publications/statistics-square-one
Question 48 |
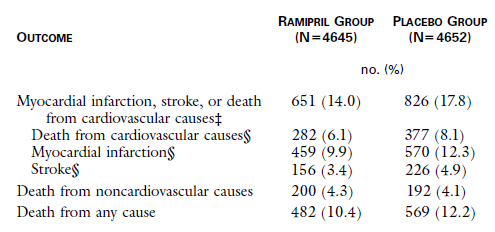Given the data above what is the relative risk of death from any cause?0.85 | |
0.20 | |
0.47 | |
0.67 |
Question 48 Explanation:
Answer A. Relative risk: 0.85
(Event rate in Ramipril group)/(Event rate in Placebo group) = (482/4645)/(569/4652) = 0.8471
Reference:
Barratt A, Wyer PC, Hatala R, et al. Tips for learners of evidence-based medicine: 1. Relative risk reduction, absolute risk reduction and number needed to treat. CMAJ. 2004;171(4):353-8. doi: 10.1503/cmaj.1021197.
(Event rate in Ramipril group)/(Event rate in Placebo group) = (482/4645)/(569/4652) = 0.8471
Reference:
Barratt A, Wyer PC, Hatala R, et al. Tips for learners of evidence-based medicine: 1. Relative risk reduction, absolute risk reduction and number needed to treat. CMAJ. 2004;171(4):353-8. doi: 10.1503/cmaj.1021197.
Question 49 |
If the relative risk of Myocardial Infarction is 0.80, what is the relative risk reduction?80% | |
20% | |
31% | |
67% |
Question 49 Explanation:
Answer B.
1 – (relative risk) =
1 – 0.80 = 0.20
Relative risk reduction: 0.20 = 20% Reference:
Barratt A, Wyer PC, Hatala R, et al. Tips for learners of evidence-based medicine: 1. Relative risk reduction, absolute risk reduction and number needed to treat. CMAJ. 2004;171(4):353-8. doi: 10.1503/cmaj.1021197.
1 – (relative risk) =
1 – 0.80 = 0.20
Relative risk reduction: 0.20 = 20% Reference:
Barratt A, Wyer PC, Hatala R, et al. Tips for learners of evidence-based medicine: 1. Relative risk reduction, absolute risk reduction and number needed to treat. CMAJ. 2004;171(4):353-8. doi: 10.1503/cmaj.1021197.
Question 50 |
Given the data above what is the relative risk reduction of stroke?80% | |
20% | |
31% | |
67% |
Question 50 Explanation:
Answer C. Relative risk reduction: 0.31 = 31%
Relative risk: (Event rate in Ramipril group)/(Event rate in Placebo group) =
(156/4645)/(226/4652) = 0.6913
1 – (relative risk) =
1 – 0.6913 = 0.3087
Reference:
Barratt A, Wyer PC, Hatala R, et al. Tips for learners of evidence-based medicine: 1. Relative risk reduction, absolute risk reduction and number needed to treat. CMAJ. 2004;171(4):353-8. doi: 10.1503/cmaj.1021197.
Relative risk: (Event rate in Ramipril group)/(Event rate in Placebo group) =
(156/4645)/(226/4652) = 0.6913
1 – (relative risk) =
1 – 0.6913 = 0.3087
Reference:
Barratt A, Wyer PC, Hatala R, et al. Tips for learners of evidence-based medicine: 1. Relative risk reduction, absolute risk reduction and number needed to treat. CMAJ. 2004;171(4):353-8. doi: 10.1503/cmaj.1021197.
Question 51 |
Given the data above what is the absolute risk reduction of death from cardiovascular causes?2.03% | |
1.03% | |
5.03% | |
20% |
Question 51 Explanation:
Answer A. Absolute risk reduction: 0.0203 = 2.03%
(Event rate in Placebo group) – (Event rate in Ramipril group)
= (377/4652) – (282/4645) = 0.02032997
Reference:
Barratt A, Wyer PC, Hatala R, et al. Tips for learners of evidence-based medicine: 1. Relative risk reduction, absolute risk reduction and number needed to treat. CMAJ. 2004;171(4):353-8. doi: 10.1503/cmaj.1021197.
= (377/4652) – (282/4645) = 0.02032997
Reference:
Barratt A, Wyer PC, Hatala R, et al. Tips for learners of evidence-based medicine: 1. Relative risk reduction, absolute risk reduction and number needed to treat. CMAJ. 2004;171(4):353-8. doi: 10.1503/cmaj.1021197.
Question 52 |
The relative risk of death from noncardiovascular causes is 1.03 with confidence interval of 95% is 0.85-1.26. Which of the following statement is true?
Death from non-cardiovascular disease was greater in placebo group compared to Ramipril group. | |
Death from non-cardiovascular disease was greater in Ramipril group compared to placebo group | |
There was no statistical significant difference between the groups. | |
Statistical significance cannot be concluded from the given data. |
Question 52 Explanation:
Answer C. A relative risk of 1.03 indicates that there is a slight increase in death from non-cardiovascular causes with treatment as compared to placebo. However, there was no statistical significant difference between the groups since the relative risk of death from non-cardiovascular causes fell within the 95% confidence interval of 0.85 to 1.26. Since the confidence interval included 1, this also indicates that there was no significant difference between the groups. If the confidence interval did not include 1, but the relative risk was greater than 1, then there would be a greater risk for death with the treatment group than the placebo group. If the confidence interval did not include 1, but the relative risk was less than 1, then there would be less risk for death with the treatment group compared to the placebo group.
Reference:
Montori VM, Kleinbart J, Newman TB, et al. Tips for learners of evidence-based medicine: 2. Measures of precision (confidence intervals). CMAJ. 2004;171(6):611-5.
Reference:
Montori VM, Kleinbart J, Newman TB, et al. Tips for learners of evidence-based medicine: 2. Measures of precision (confidence intervals). CMAJ. 2004;171(6):611-5.
Question 53 |
How many patients would you have to treat with Ramipril to prevent 1 death from cardiovascular cause?39 | |
59 | |
51 | |
49 |
Question 53 Explanation:
Answer D. Number needed to treat: 49
1/(absolute risk reduction) =
1/0.02032997 = 49.18846
Reference:
Barratt A, Wyer PC, Hatala R, et al. Tips for learners of evidence-based medicine: 1. Relative risk reduction, absolute risk reduction and number needed to treat. CMAJ. 2004;171(4):353-8. doi: 10.1503/cmaj.1021197.
1/(absolute risk reduction) =
1/0.02032997 = 49.18846
Reference:
Barratt A, Wyer PC, Hatala R, et al. Tips for learners of evidence-based medicine: 1. Relative risk reduction, absolute risk reduction and number needed to treat. CMAJ. 2004;171(4):353-8. doi: 10.1503/cmaj.1021197.
Question 54 |
What is the absolute risk increase using Dronedarone compared to placebo?170% | |
30% | |
6.9% | |
4.9% |
Question 54 Explanation:
Answer D.
Absolute risk increase: 0.049 = 4.9%
(Event rate in Placebo group) – (Event rate in Dronedarone group)
= (9/317) – (24/310) = - 0.049028
Reference:
Barratt A, Wyer PC, Hatala R, et al. Tips for learners of evidence-based medicine: 1. Relative risk reduction, absolute risk reduction and number needed to treat. CMAJ. 2004;171(4):353-8. doi: 10.1503/cmaj.1021197.
(Event rate in Placebo group) – (Event rate in Dronedarone group)
= (9/317) – (24/310) = - 0.049028
Reference:
Barratt A, Wyer PC, Hatala R, et al. Tips for learners of evidence-based medicine: 1. Relative risk reduction, absolute risk reduction and number needed to treat. CMAJ. 2004;171(4):353-8. doi: 10.1503/cmaj.1021197.
Question 55 |
What is the number needed to harm?20 | |
80 | |
60 | |
40 |
Question 55 Explanation:
Answer A. Number needed to harm: 20
1/(absolute risk increase) = 1/0.049 = 20.3965
Reference:
Barratt A, Wyer PC, Hatala R, et al. Tips for learners of evidence-based medicine: 1. Relative risk reduction, absolute risk reduction and number needed to treat. CMAJ. 2004;171(4):353-8. doi: 10.1503/cmaj.1021197.
1/(absolute risk increase) = 1/0.049 = 20.3965
Reference:
Barratt A, Wyer PC, Hatala R, et al. Tips for learners of evidence-based medicine: 1. Relative risk reduction, absolute risk reduction and number needed to treat. CMAJ. 2004;171(4):353-8. doi: 10.1503/cmaj.1021197.
Question 56 |
A study had 11,000 healthy patients, 4 years later 212 developed the disease. What is the best estimated incidence rate of disease over the study period? Report your answer per 1000 person-years
19 cases per 1,000 person-years | |
9 cases per 1,000 person-years | |
1.9 cases per 1,000 person-years | |
4.8 cases per 1,000 person-years |
Question 56 Explanation:
Answer D. Incidence rate = New reported cases / summed person-years of observation (avg population during time interval)
11,000 people x 3 years = 33,000 11,000 – 212 = 10,788
Incidence rate = 212 / ((10,788 + ½ 212) + 33,000) = 0.0048 cases per person-year
0.0048 cases per person-year x 1000 = 4.8 cases per 1,000 person-years
Reference:
Dicker, R. C., Coronado, F., Koo, D., et al. Principals of Epidemiology in Public Health Practice, Third Edition: An Introduction to Applied Epidemiology and Biostatistics; Lesson 3, Section 2. Oct. 2006 Retrieved Jan. 24, 2017 from: https://www.cdc.gov/ophss/csels/dsepd/ss1978/lesson3/section2.html Updated: Nov. 2011
11,000 people x 3 years = 33,000 11,000 – 212 = 10,788
Incidence rate = 212 / ((10,788 + ½ 212) + 33,000) = 0.0048 cases per person-year
0.0048 cases per person-year x 1000 = 4.8 cases per 1,000 person-years
Reference:
Dicker, R. C., Coronado, F., Koo, D., et al. Principals of Epidemiology in Public Health Practice, Third Edition: An Introduction to Applied Epidemiology and Biostatistics; Lesson 3, Section 2. Oct. 2006 Retrieved Jan. 24, 2017 from: https://www.cdc.gov/ophss/csels/dsepd/ss1978/lesson3/section2.html Updated: Nov. 2011
Question 57 |
Dresner County’s tuberculosis registry indicated there were 9 new cases and 356 pre-existing cases of TB in 2016. The population of Dresner County is 410,200 people. What is the prevalence of TB in Dresener County in 2016? What is the incidence rate of TB in Dresner County in 2016 per 100,000 patients?
0.89%; 22 cases per 100,000 person-years | |
8.9%; 22 cases per 100,000 person-years | |
0.89%; 2.2 cases per 100,000 person-years | |
0.089%; 2.2 cases per 100,000 person-years |
Question 57 Explanation:
Answer D. Prevalence = Cases in a population in a given time period / total population at that time
Prevalence in 2016 = (356 + 9) / 410,200 = 0.00089 x 100 = 0.089%
Incidence rate = New reported cases / summed person-years of observation (avg population during time interval)
Incidence rate = 9 / (409,835 + ½ 9) = 0.000022 x 100,000 = 2.2 cases per 100,000 person-years
Reference:
Dicker, R. C., Coronado, F., Koo, D., et al. Principals of Epidemiology in Public Health Practice, Third Edition: An Introduction to Applied Epidemiology and Biostatistics; Lesson 3, Section 2. Oct. 2006 Retrieved Jan. 24, 2017 from: https://www.cdc.gov/ophss/csels/dsepd/ss1978/lesson3/section2.html Updated: Nov. 2011
Numerators, denominators and populations at risk. Jun. 20, 2010. Retrieved Jan. 24, 2017 from: http://www.healthknowledge.org.uk/public-health-textbook/research-methods/1a-epidemiology/numerators-denominators-populations
Incidence rate = New reported cases / summed person-years of observation (avg population during time interval)
Incidence rate = 9 / (409,835 + ½ 9) = 0.000022 x 100,000 = 2.2 cases per 100,000 person-years
Reference:
Dicker, R. C., Coronado, F., Koo, D., et al. Principals of Epidemiology in Public Health Practice, Third Edition: An Introduction to Applied Epidemiology and Biostatistics; Lesson 3, Section 2. Oct. 2006 Retrieved Jan. 24, 2017 from: https://www.cdc.gov/ophss/csels/dsepd/ss1978/lesson3/section2.html Updated: Nov. 2011
Numerators, denominators and populations at risk. Jun. 20, 2010. Retrieved Jan. 24, 2017 from: http://www.healthknowledge.org.uk/public-health-textbook/research-methods/1a-epidemiology/numerators-denominators-populations
Question 58 |
Due to contamination of water supply in a small town there were several outbreak of gastroenteritis. 1650 people drank the supply water of which 250 had gastroenteritis, 1540 people drank the bottled water of which 3 people had gastroenteritis. Construct a contingency table. What is the odds ratio(OR)? What is the relative risk(RR)?
OR=17.85, RR=15.15 | |
OR=91.5, RR=77.78 | |
OR=8.7, RR=7.83 | |
OR=0.21, RR=0.19 |
Question 58 Explanation:
Answer B.
No Gastroenteritis Gastroenteritis
Water Supply 1400 250
Bottled Water 1537 3
Risk Ratio = Rate of Gastroenteritis in patients drinking water supply / rate in patients drinking bottled
Relative Risk = (250/1650) / (3/1540) = 77.78
Odds = Number of patients with illness / Number of patients without illness
Odds ratio = One group / Other group
Odds ratio = (250/1400) / (3/1537) = 91.5 Another formula used for the odds ratio is: Odds ratio = (exposed cases / unexposed cases) / (exposed non-cases / unexposed non-cases)
In this equation exposed patients are patients that drank from the water supply and unexposed patients are patients that drank from water bottles. Cases are patients that had gastroenteritis and non-cases are patients that did not have the illness present.
Reference:
2x2 Contingency Table with Odds Ratios, etc. (n.d.). Retrieved Jan. 24, 2017 from: http://www.vassarstats.net/odds2x2.html
Szumilas, M. "Explaining odds ratios." J Can Acad Child Adolesc Psychiatry 19 (2010): 227. Retrieved Jan. 24, 2017 from: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2938757/
No Gastroenteritis Gastroenteritis
Water Supply 1400 250
Bottled Water 1537 3
Risk Ratio = Rate of Gastroenteritis in patients drinking water supply / rate in patients drinking bottled
Relative Risk = (250/1650) / (3/1540) = 77.78
Odds = Number of patients with illness / Number of patients without illness
Odds ratio = One group / Other group
Odds ratio = (250/1400) / (3/1537) = 91.5 Another formula used for the odds ratio is: Odds ratio = (exposed cases / unexposed cases) / (exposed non-cases / unexposed non-cases)
In this equation exposed patients are patients that drank from the water supply and unexposed patients are patients that drank from water bottles. Cases are patients that had gastroenteritis and non-cases are patients that did not have the illness present.
Reference:
2x2 Contingency Table with Odds Ratios, etc. (n.d.). Retrieved Jan. 24, 2017 from: http://www.vassarstats.net/odds2x2.html
Szumilas, M. "Explaining odds ratios." J Can Acad Child Adolesc Psychiatry 19 (2010): 227. Retrieved Jan. 24, 2017 from: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2938757/
Question 59 |
In a cohort study where they looked at association of low dose aspirin on cardiovascular events in 39 876 female health professionals (mean age 54 years), investigators found (relative risk [RR] 0.91, 95% confidence interval [CI] 0.80 to 1.03). Risk of hemorrhagic stroke in the ASA group (RR 1.24, 95% CI 0.82 to 1.87). Among women 65 years old or older, subgroup analyses showed (RR 0.74, 95% CI 0.59 to 0.92) for major CV events.
Which of the following is correct interpretation of this finding?
Use of low dose aspirin reduces cardiovascular events by 9% in female health professionals | |
Use of low dose aspirin reduces cardiovascular events by 91% in female health professionals | |
Use of low dose aspirin did not reduce cardiovascular events in female health professionals | |
Use of low dose aspirin reduces cardiovascular events by 0.91% in female health professionals |
Question 59 Explanation:
Answer C. In this study, looking at the RR it may seem like the ASA group had a reduced risk for CVE, but once the 95% CI is taken into account, the results do not seem significant because the interval spans the value 1, which would indicating the null cannot be rejected (i.e. there is no difference between groups). The 95% CI is basically telling us that we can be 95% sure the true value lies between the given interval, when the interval contains the value 1 it is difficult to refute the null if it falls in that 95% certainty range.
Reference:
Irwig, Les. Chapter 18: Relative risk, relative and absolute risk reduction, number needed to treat and confidence intervals. Smart health choices: making sense of health advice. Judy Irwig, 2007. Retrieved Jan. 24, 2017 from: https://www.ncbi.nlm.nih.gov/books/NBK63647/
Confidence Intervals for the Risk Ratio (Relative Risk). (n.d.) Retrieved Jan. 24, 2017 from: http://sphweb.bumc.bu.edu/otlt/mph-modules/bs/bs704_confidence_intervals/bs704_confidence_intervals8.html
Reference:
Irwig, Les. Chapter 18: Relative risk, relative and absolute risk reduction, number needed to treat and confidence intervals. Smart health choices: making sense of health advice. Judy Irwig, 2007. Retrieved Jan. 24, 2017 from: https://www.ncbi.nlm.nih.gov/books/NBK63647/
Confidence Intervals for the Risk Ratio (Relative Risk). (n.d.) Retrieved Jan. 24, 2017 from: http://sphweb.bumc.bu.edu/otlt/mph-modules/bs/bs704_confidence_intervals/bs704_confidence_intervals8.html
Question 60 |
In a cohort study where they looked at association of low dose aspirin on cardiovascular events in 39 876 female health professionals (mean age 54 years), investigators found (relative risk [RR] 0.91, 95% confidence interval [CI] 0.80 to 1.03). Risk of hemorrhagic stroke in the ASA group (RR 1.24, 95% CI 0.82 to 1.87). Among women 65 years old or older, subgroup analyses showed (RR 0.74, 95% CI 0.59 to 0.92) for major CV events.
Which of the following is correct interpretation of this finding?
Women who used low dose aspirin had a 0.26 times risk of major cardiovascular events | |
Use of low dose aspirin was associated with a 74% reduction in risk of major cardiovascular events in women 65 years or older. | |
Women who used low dose aspirin had a 0.74 times risk of major cardiovascular events | |
Use of low dose aspirin was associated with a 26% reduction in risk of major cardiovascular events in women 65 years or older. |
Question 60 Explanation:
Answer D. In this study, looking at the RR it may seem like the ASA group had an increased risk for hemorrhagic stroke, but once the 95% CI is taken into account, the results do not seem significant because the interval spans the value 1, which would indicating the null cannot be rejected (i.e. there is no difference between groups). The 95% CI is basically telling us that we can be 95% sure the true value lies between the given interval, when the interval contains the value 1 it is difficult to refute the null if it falls in that 95% certainty range.
Reference:
Irwig, Les. Chapter 18: Relative risk, relative and absolute risk reduction, number needed to treat and confidence intervals. Smart health choices: making sense of health advice. Judy Irwig, 2007. Retrieved Jan. 24, 2017 from: https://www.ncbi.nlm.nih.gov/books/NBK63647/
Confidence Intervals for the Risk Ratio (Relative Risk). (n.d.) Retrieved Jan. 24, 2017 from: http://sphweb.bumc.bu.edu/otlt/mph-modules/bs/bs704_confidence_intervals/bs704_confidence_intervals8.html
Reference:
Irwig, Les. Chapter 18: Relative risk, relative and absolute risk reduction, number needed to treat and confidence intervals. Smart health choices: making sense of health advice. Judy Irwig, 2007. Retrieved Jan. 24, 2017 from: https://www.ncbi.nlm.nih.gov/books/NBK63647/
Confidence Intervals for the Risk Ratio (Relative Risk). (n.d.) Retrieved Jan. 24, 2017 from: http://sphweb.bumc.bu.edu/otlt/mph-modules/bs/bs704_confidence_intervals/bs704_confidence_intervals8.html
Question 61 |
The ratio of the probability of an event occurring in an exposed group to the probability of the event occurring in a non-exposed group is definition of which of the following?
Incidence rate | |
Prevalence rate | |
Odds ratio | |
Relative risk |
Question 61 Explanation:
Answer C. Odds ratio = (exposed cases / unexposed cases) / (exposed non-cases / unexposed non-cases)
Reference:
Szumilas, M. "Explaining odds ratios." J Can Acad Child Adolesc Psychiatry 19 (2010): 227. Retrieved Jan. 24, 2017 from: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2938757/
Reference:
Szumilas, M. "Explaining odds ratios." J Can Acad Child Adolesc Psychiatry 19 (2010): 227. Retrieved Jan. 24, 2017 from: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2938757/
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 61 questions to complete.
|
List |
Comments are closed.